A Binary Search Tree is a container data structure, that keeps its keys always sorted. Any given node is greater than or equal to any key stored in the left sub-tree, and less than or equal to any key stored in the right sub-tree.

Search, Delete and Insert operations are proportional to the height of the tree. In average, binary search complexity is O(log(n)), but in the worst case, we are basically dealing with a singly linked list, and search is O(n).

Unbalanced BST

So, as you can see, in order to obtain best results, BSTs should be balanced. And, by balanced, we mean that the height should be log(n).

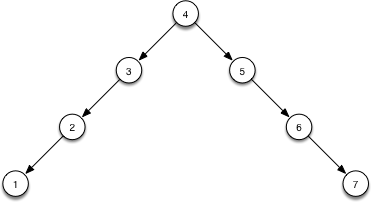
So, let’s start with the degenerate case:

Degenerate BST

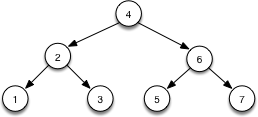
Is easy to see that, search here will take O(n), and is also easy to see that if we can rotate the whole tree around the middle (4 in this case), then we would be reducing the height in half. It turns out that that’s all we need. We need to convert the unbalanced BST to the degenerate case, and then perform rotations around the middle point of each subtree.

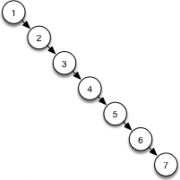
But how to get the degenerate case? Again, fairly easy. By the very structure of the BST, if we traverse the tree in-order, the resulting data structure is the degenerate tree (or a representation of it. For instance, in the playground attached, I’ve chosen to dump everything to an array because after obtaining the list, we need to manipulate it accessing elements at random. A linked list or a tree will be enough, but an array is far better to access the element in the nth position. An important consideration, if we are dealing with a huge tree, then it would be better to manipulate the tree in place to save memory).

Once we have the degenerate tree, all we need to do is to keep rotating around the middle point of each sub-tree, until we are done. And the very best is that by the structure of any tree, recursion is almost mandatory.

func sortedArrayToBST(_ sortedArray: [T], start: Int, end: Int) -> BinarySearchTree<T> {
        if start > end {
            return BinarySearchTree.empty
        }

        let middle = (start + end) / 2

        let left = sortedArrayToBST(sortedArray, start: start, end: middle - 1)
        let right = sortedArrayToBST(sortedArray, start: middle + 1, end: end)

        let root = BinarySearchTree.node(left, sortedArray[middle], right)

        return root
    }

Balanced BST